ナイル川の氾濫は「ピタゴラスの定理」と繋がっています。 「なにこれ?」と思う人が多いでしょうね。 ピタゴラスの定理の原点はエジプト・ナイル川の測量術と繋がるのです。 日常
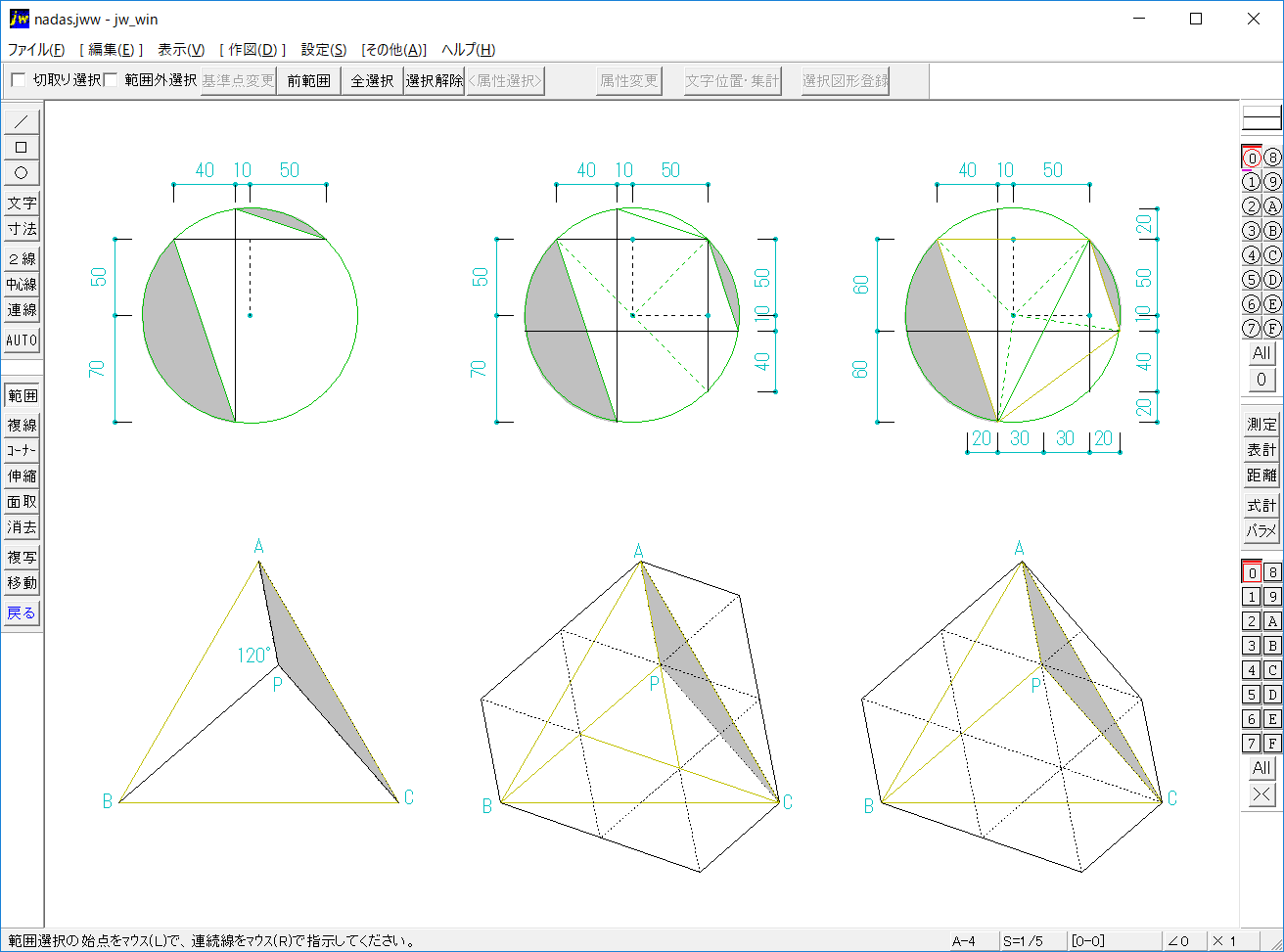
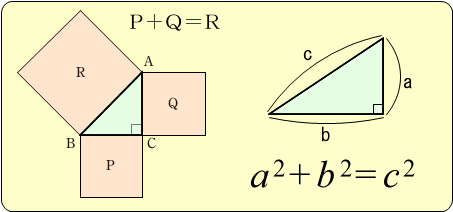
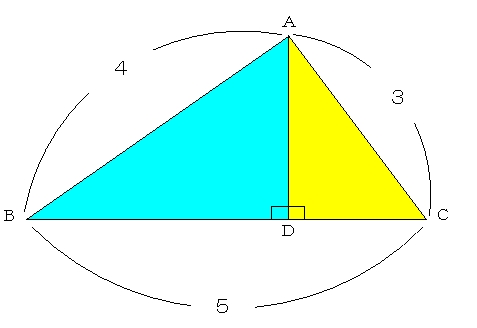
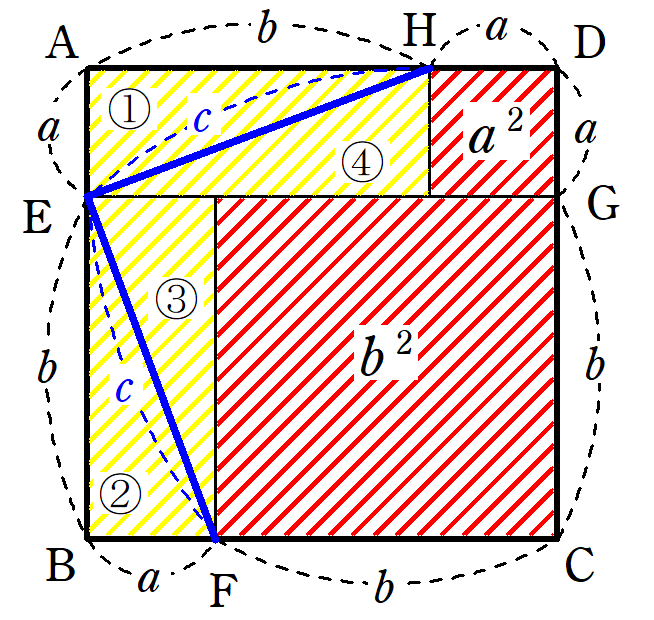
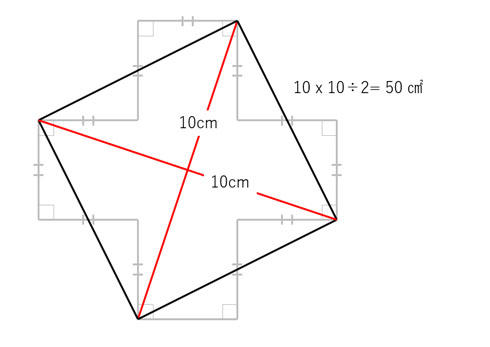
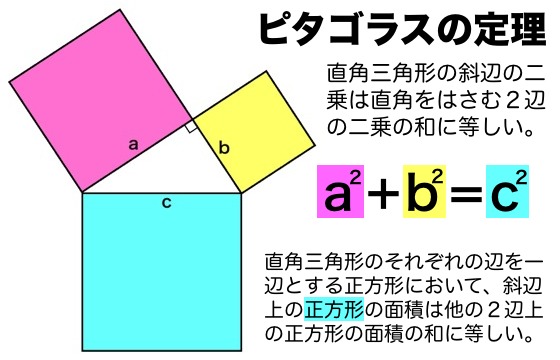
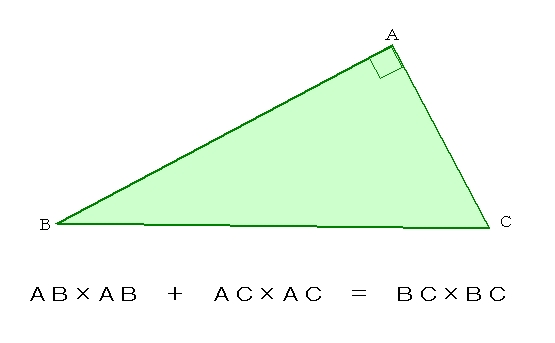
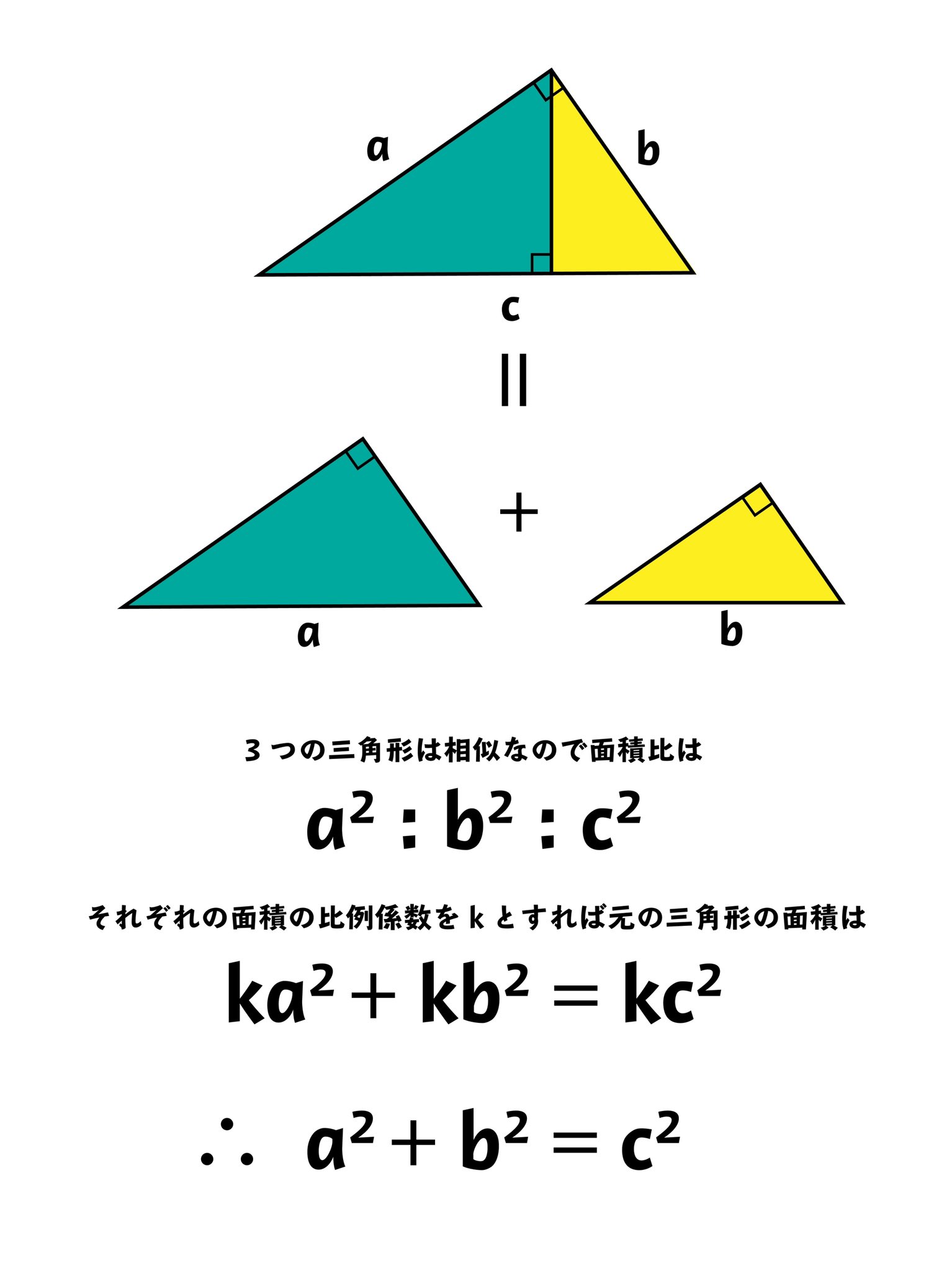
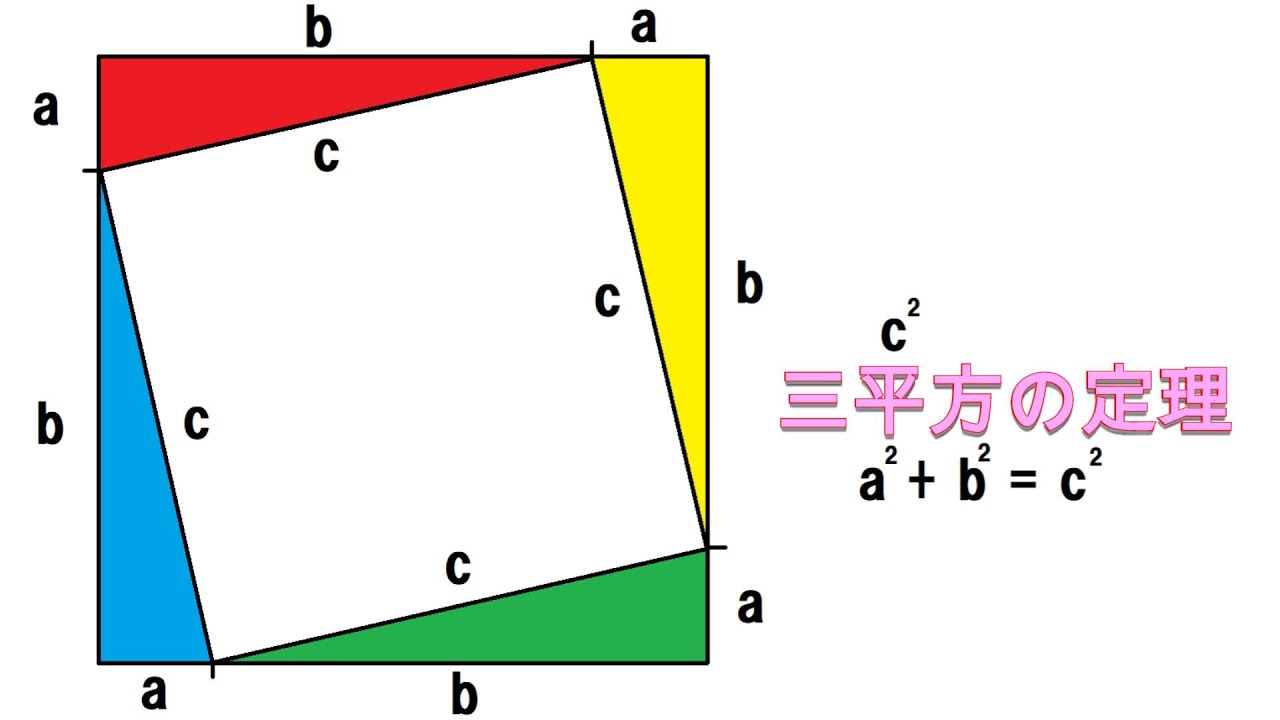
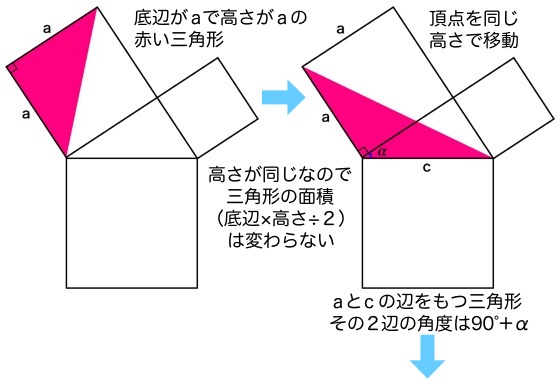
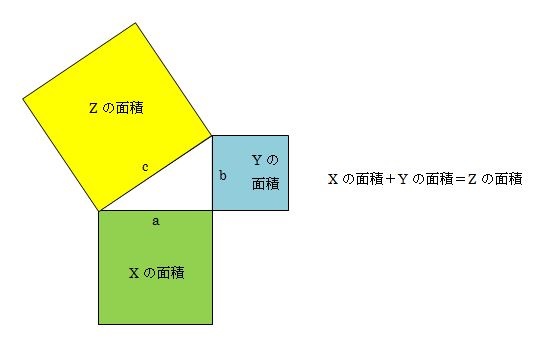
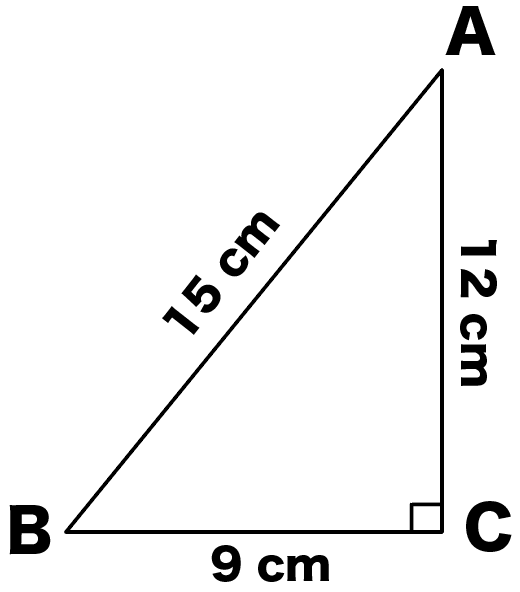
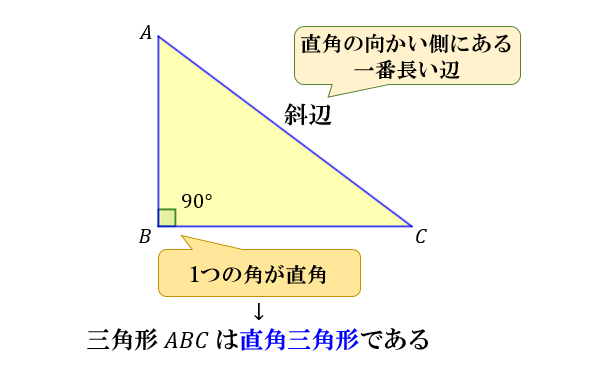
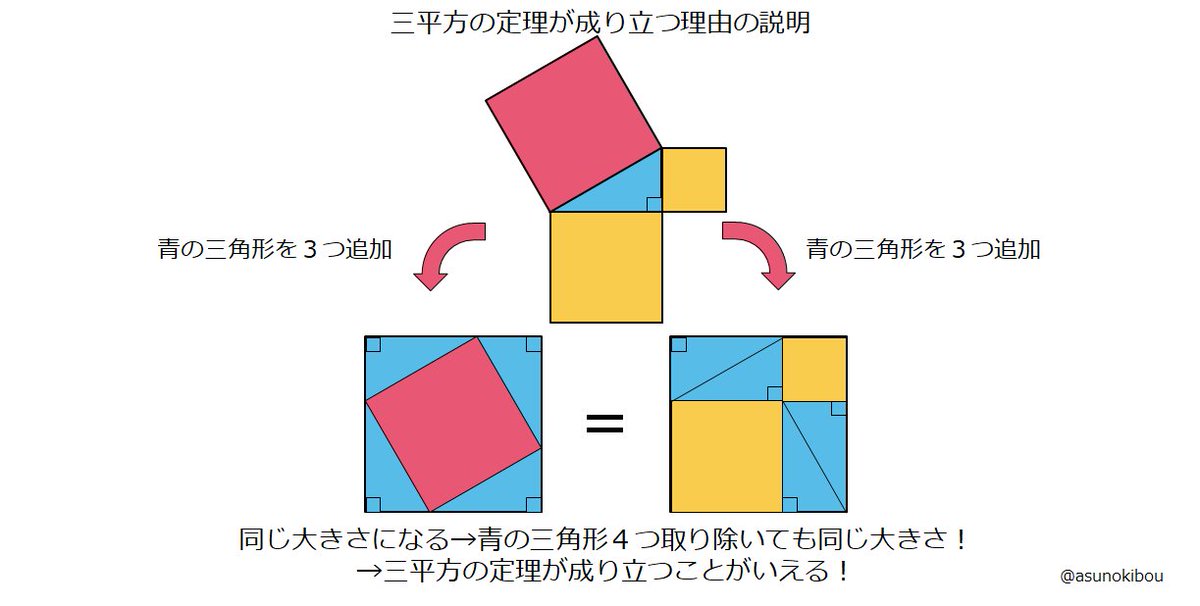
ピタゴラスの定理 小学生用- 大きな正方形=小さな正方形+直角三角形×4 になっていることに注目すると、大きな正方形の一辺は a b 、小さな正方形の一辺は c ですから、 (a b)2 = c2 1 2ab × 4 展開すると 以下にこの定理の証明方法を載せておくので、興味のある方はぜひ読んでもらえると解説に説得力がつくと思います。 (証明) ピタゴラスの定理から、 ・・・① また、二つの三日月型
ピタゴラスの定理 小学生用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
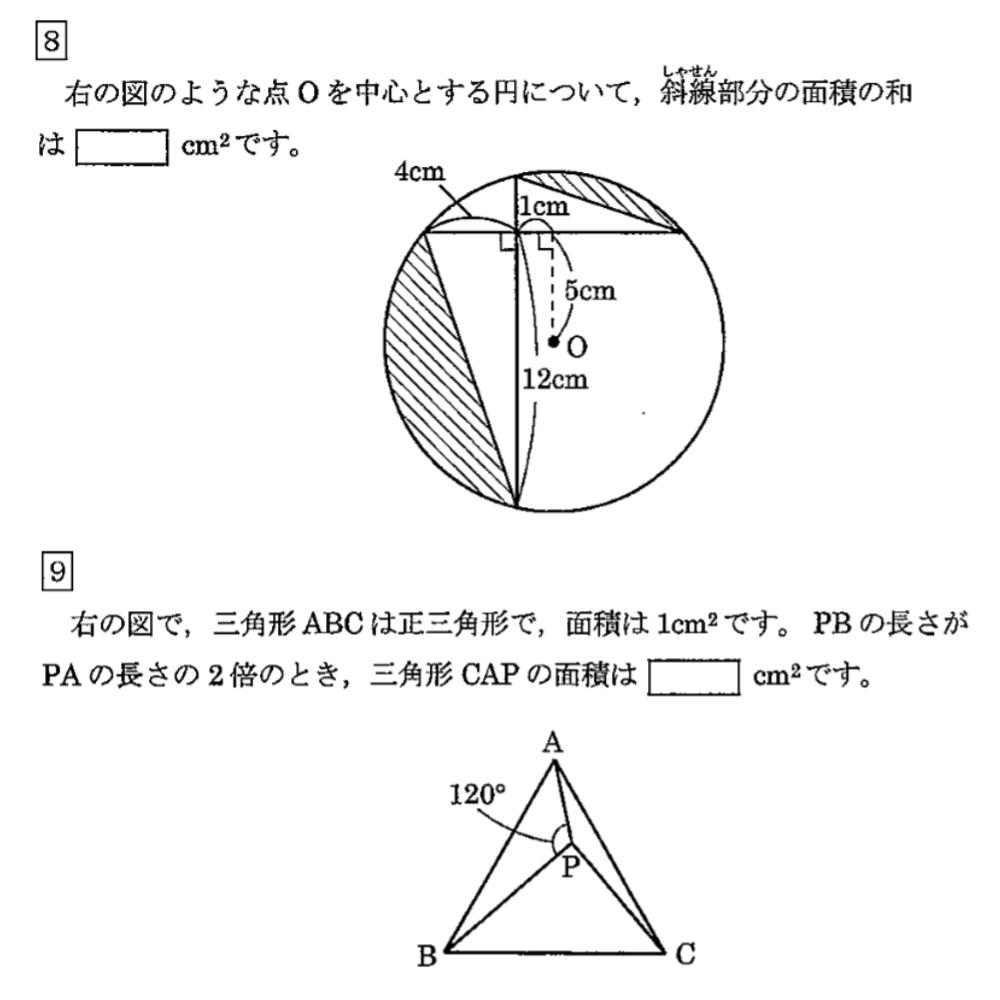 | ||
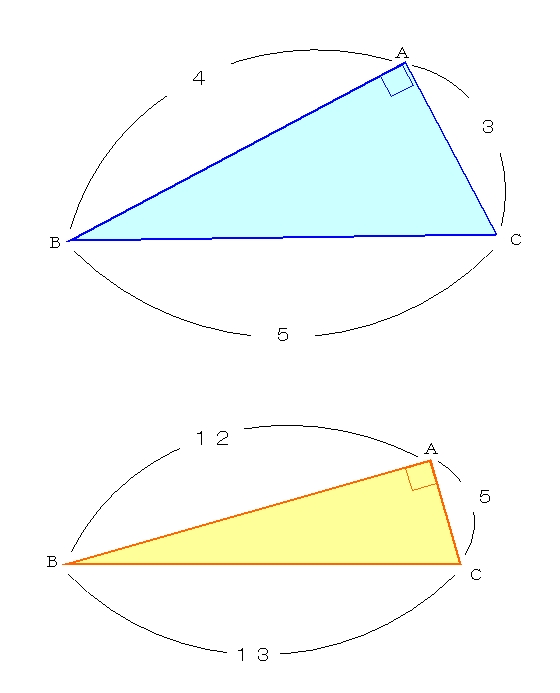 |  | |
 | 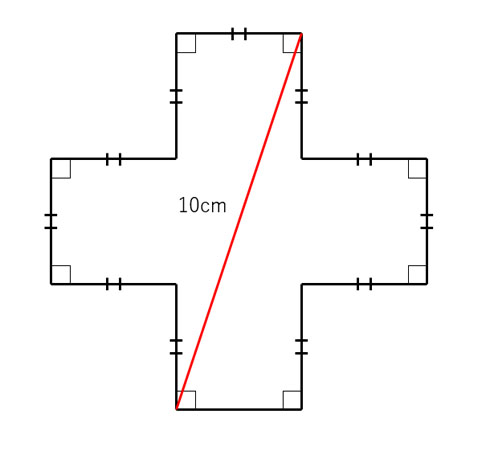 |  |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  | |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
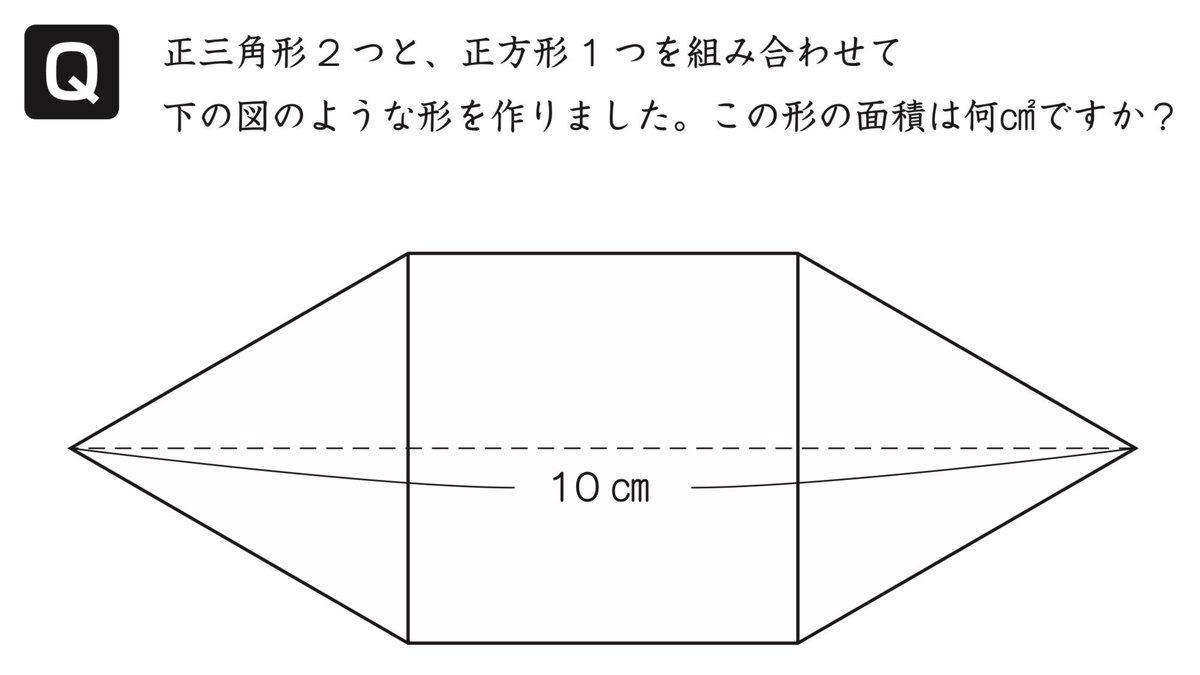 | ||
 |  |  |
 |  |  |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
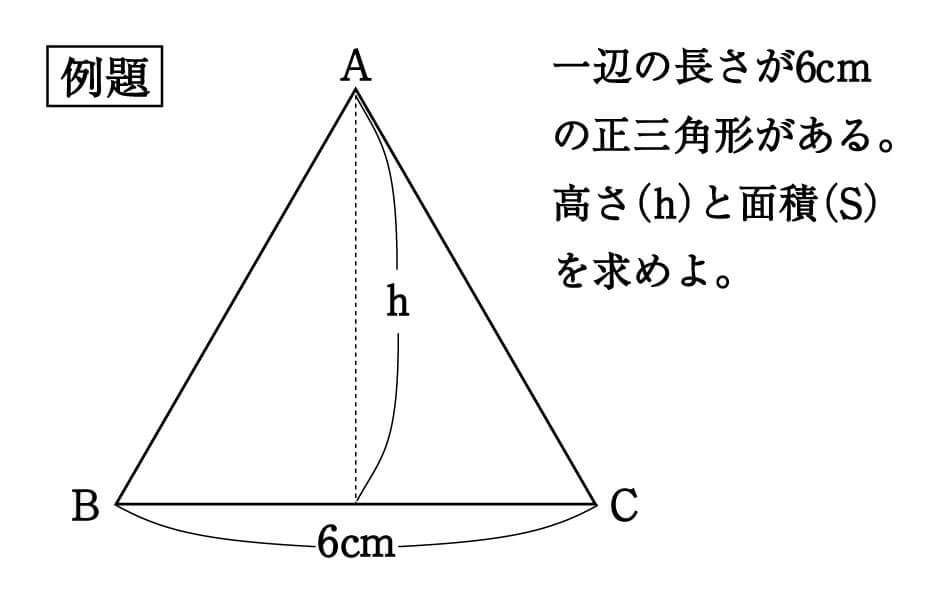 | 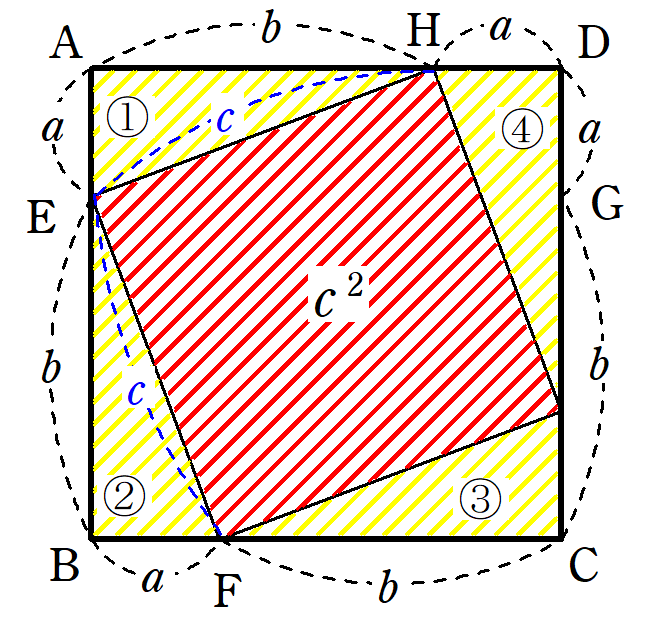 | |
 |  |  |
 |  |  |
「ピタゴラスの定理 小学生用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
ピタゴラスの定理の一つの証明法(原 憲昭) rarc rr kanc >&13>' ― 2 ― ah が接角を2直角に等しくする。 それゆえΓa は ah と一直線をなす。 同じ理由で ba もaΘと一 直線をなす。そして角ΔbΓ 中1の1学期に実践する「ピタゴラスの定理」とは? 一昨日お届けした数学の授業紹介。 その中で明星学園中学校では、中1の1学期に「ピタゴラスの定理」を学ぶとお伝えしました。 け
Incoming Term: ピタゴラスの定理 小学生, ピタゴラスの定理 小学生用, ピタゴラスの定理 1 2 ルート3,




0 件のコメント:
コメントを投稿